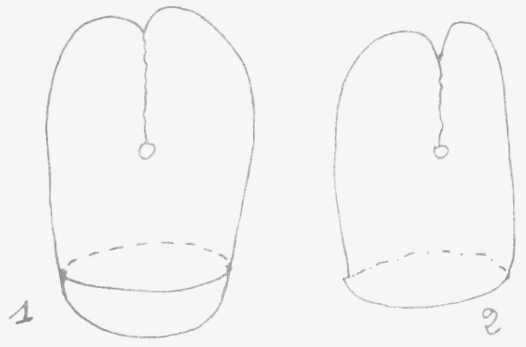
Ces trois surfaces, sphère, tore, cross-cap sont des surfaces closes élémentaires à la composition desquelles toutes les autres surfaces closes peuvent se réduire.
IX-L'IDENTIFICATION
Séminaire du 16 mai 1962
(Rédaction d'après des notes)
(->p436) (XX/1)
Cette élucubration de la surface, j'en justifie la nécessité, il est évident que ce que je vous en donne est le résultat d'une réflexion. Vous n'avez pas oublié que la notion de surface en topologie ne va pas de soi et n'est pas donnée comme une intuition. La surface est quelque chose qui ne va pas de soi.
Comment l'aborder ? à partir de ce qui dans le réel l'introduit, c'est-à-dire qui montrerait que l'espace n'est pas cette étendue ouverte et méprisable comme le pensait Bergson. L'espace n'est pas si vide qu'il croyait, il recèle bien des mystères.
Posons au départ certains termes.
Il est certain qu'une première chose essentielle dans la notion de surface est celle de face : il y aurait 2 faces ou 2 cotés. Cela va de soi si, cette surface, nous la plongeons dans l'espace. Mais pour nous approprier ce que peut pour nous prendre la notion de surface, il faut que nous sachions ce qu'elle nous livre de ses seules dimensions, voir ce qu'elle peut nous livrer en tant que surface divisant l'espace de ses seules dimensions, nous suggère de reconstruire l'espace autrement que nous croyions en avoir l'intuition. En d'autres termes, je vous propose de considérer comme plus évident (capture imaginaire), plus certain (lié à l'action) , plus structural de partir de la surface pour définir l'espace - dont je tiens que nous sommes peu assurés - disons plutôt définir le lieu, que de partir du lieu pour définir la surface - c'est le lieu en philosophie - le lieu de l'Autre a déjà sa place dans notre séminaire. Pour définir la face d'une surface, il ne suffit pas de dire que c'est d'un côté et de l'autre, d'autant plus que ça n'a rien de satisfaisant, et si quelque chose nous donne le vertige (->p437) (XX/2) pascalien, c'est bien ces 2 régions dont le plan infini diviserait tout l'espace.
Comment définir cette notion de face ? c'est le champ où peut s'étendre une ligne, un chemin sans avoir à rencontrer un bord. Mais il y a des surfaces sans bord : le plan à l'infini, la sphère, le tore et plusieurs autres qui comme surface sans bord se réduisent pratiquement à une seule : le cross-cap ou mitre ou bonnet figuré ci-contre (1)
|
|
Le cross-cap dans
les livres savants c'est ça : coupé pour pouvoir s'insérer sur
une autre surface (2)
Ces trois surfaces, sphère, tore, cross-cap sont des surfaces closes élémentaires à la composition desquelles toutes les autres surfaces closes peuvent se réduire. |
J'appellerai
néanmoins cross-cap la figure 1. Son vrai nom est le plan projectif de la
théorie des surfaces de Riemann dont le plan est la base. Il fait intervenir
au moins la quatrième dimension.
Déjà la 3ème dimension, pour nous
psychologues des profondeurs fait assez problème pour que nous la considérions
comme peu assurée. Néanmoins dans cette simple figure, le cross-cap, la 4 eme
est déjà impliquée nécessairement.
Le noeud élémentaire fait l'autre jour avec une ficelle présentifie déjà la 4 eme dimension. Il n'y a pas de théorie topologique valable sans que nous fassions intervenir quelque chose qui nous mènera à la 4 eme dimension.
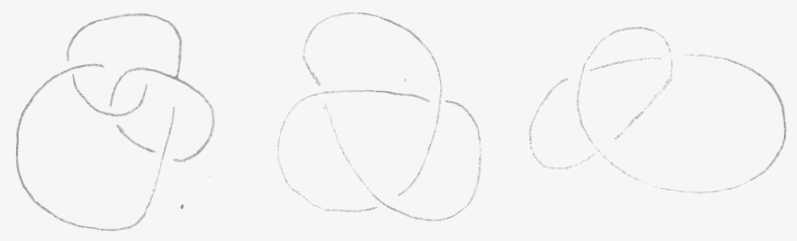
Si, ce noeud, vous voulez essayer de le reproduire en usant du tore en suivant les tours et les détours que vous pouvez faire à la surface d'un tore, vous pourriez après plusieurs tours revenir sur une ligne qui se boucle comme le noeud ci-dessus. Vous ne pouvez le faire sans que la ligne se coupe elle-même; comme la surface du tore vous ne pouvez pas marquer que la ligne passe au-dessus ou au-dessous, il n'y a pas moyen de faire ce noeud sur le tore. Il est par contre parfaitement faisable sur le cross-cap. Si cette surface implique la présence de la 4 eme dimension, c'est un commencement de preuve que le plus simple noeud implique la 4 eme dimension. Cette surface, le cross-cap, je vais vous dire comment vous pouvez l'imaginer. Ca n'imposera pas sa nécessité par là même, pour nous, menée. Elle n'est pas sans rapport avec le tore, elle a même avec le tore le rapport le plus profond. La façon la plus simple de vous donner ce rapport est de vous rappeler comment un tore est construit quand on le décompose sous une forme polyédrique, c'est-à-dire en le ramenant à son polygone fondamental. Ici ce polygone fondamental, c'est un quadrilatère. Si ce quadrilatère vous le repliez
|
|
sur lui-même, vous aurez un tube en
joignant les bords. Si on vectorise ces bords en convenant que ne peuvent
être accolés l'un à l'autre que les vecteurs qui vont dans le même
sens, le début d'un vecteur s'appliquant au point où se termine l'autre
vecteur, dés lors on a toutes les coordonnées pour définir la structure
du tore.
|
Si vous faites une surface dont le polygone fondamental est ainsi défini par des vecteurs allant tous dans le même sens sur le quadrilatère de base, si vous partez d'un polygone ainsi défini, ça ferait 2 bords ou même un seul, vous obtenez ce que je vous matérialise, comme la mitre.
Je reviendrai sur la fonction de symbolisation de quelque chose et ça sera plus clair quand ce nom servira de support.
En coupe avec sa gueule de mâchoire, ça n'est pas ce que vous croyez, ceci est une ligne de pénétration grâce à quoi ce qui est en avant...
(->p439) (XX/4)
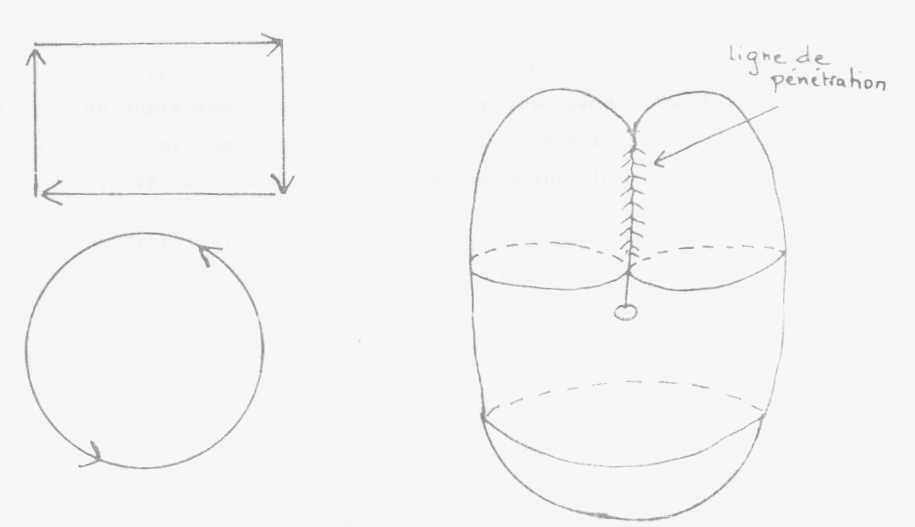
Au dessous est une demi-sphère,
en haut de la paroi avant passe par pénétration dans la paroi opposée et
revient en avant.
Pourquoi cette forme plutôt qu'une
autre ? : Son polygone fondamental est distinct de celui du tore. Un polygone,
dont les bords sont marqués par des vecteurs de même direction, et distinct de
celui du tore, qui part d'un point pour aller au point opposé, qu'est-ce que
ça fait comme surface ?
|
|
Dès maintenant, se dégagent des points problématiques de ces surfaces. Je vous ai introduit les surfaces sans bord à propos de la face. S'il n'y a pas de bord, comment définir la face ? Et si nous interdisons autant que possible de plonger trop vite notre modèle dans la 3eme dimension, là où il n'y a pas de bord nous serons assurés qu'il y a un intérieur et un extérieur. C'est ce que suggère cette surface sans |
bord par excellence qu'est la sphère. Je veux vous détacher de cette intuition indécise : il y a ce qui est au dedans et ce qui est au dehors.
Pourtant pour les autres surfaces, cette notion d'intérieur et d'extérieur se
dérobe. Pour le plan infini, elle ne suffirai pas. Pour le tore, l'intuition
colle en apparence suffisamment parce qu'il y a l'intérieur d'une chambre à
air et l'extérieur. Néanmoins ce qui se passe dans le champ où cet espace
extérieur traverse le tore, c'est-(->p440)
(XX/5)-à-dire le trou central, là
est le
nerf topologique de ce qui a fait l'intérêt du tore et où le rapport de l'intérieur
et de l'extérieur s'illustre de quelque chose qui peut nous toucher.
Remarquez que jusqu'à Freud, l'anatomie
traditionnelle, un tant soit peu Wissenschaft avec Paracelse et Aristote, a
toujours fait
La théorie
psychanalytique, en tant
que structurée par la fonction de la libido, a fait un choix bien étroit
parmi les orifice et ne nous parle pas des orifices sensoriels comme
orifices, sinon à les ramener au signifiant des orifices d'abord choisis. Quant
on fait de la scoptophilie une scoptofagie , on dit que l'identification
scoptophile est une identification orale, comme le fait Fénichel.
Le
privilège des orifices oraux, anaux
et génitaux nous retient en ceci que ce ne sont pas vraiment les orifices qui
donnent sur l'intérieur du corps : le tube digestif n'est qu'une traversée, il
est ouvert sur l'extérieur. Le vrai intérieur est l'intérieur mésodermique
et les orifices qui y introduisent existent :sous la forme des yeux ou de
l'oreille dont jamais la théorie psychanalytique ne fait mention comme tels
sauf sur la couverture de "La Psychanalvse". C'est la
vraie portée donnée au trou central du tore ; encore que ce ne soit pas un véritable
intérieur, mais que ça nous suggère quelque chose de l'ordre d'un passage de
l'intérieur à l extérieur..
|
|
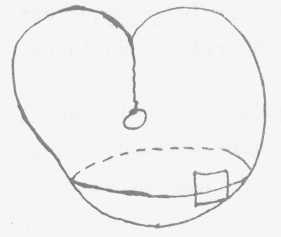
Ceci nous donne l'idée qui vient à
l'inspection de cette surface close, le cross-cap. Supposez quelque
chose d'infiniment plat qui se déplace sur cette surface passant de
l'extérieur 1 de la surface close à l'intérieur 2 pour suivre plus loin
à l'intérieur 3 de la ligne de pénétration où il ressurgira à
l'extérieur 4 (de dos)
Ceci montre la difficulté de la définition de la distinction intérieur-extérieur, même quand il s'agit d'une surface close, d'une surface sans bords.
|
(->p441) (XX/6)
Je n'ai fait qu'ouvrir là question pour
vous montrer que l'important dans cette figure c'est que cette ligne de pénétration
doit être tenue pour vous pour nulle et non avenue. On ne peut la matérialiser
au tableau sans faire intervenir cette ligne de pénétration, car l'intuition
spatiale ordinaire exige qu'on le montre, mais la spéculation n'en tient aucun
compte. On peut la faire glisser indéfiniment, cette ligne de pénétration. Il
n'y a rien de l'ordre d'une couture. Il n'y a pas de passage possible. A cause
de cela, le problème de l'intérieur et de l'extérieur est soulevé dans toute
sa confusion.
Il y a deux ordres de considération
quant à la surface : métrique et topologique. I1 faut renoncer à toute considération
métrique : en effet à partir de ce carré, je pourrais donner toute
la surface. D'un point de vue topologique, cela n'a aucun sens.
Topologiquement la nature des rapports structuraux qui constituent la surface
est présente en chaque point : la face interne se confond avec 1a face extérieure
pour chacun de ses points et de ses propriétés.
Pour marquer l'intérêt
de ceci, nous
allons évoquer une question encore jamais posée qui concerne le signifiant :
un signifiant n'a-t-il pas toujours pour lieu une surface. Ca
peut paraître une question bizarre. Mais elle a au moins l'intérêt, si elle est posée, de suggérer une dimension. Au premier abord le graphique comme
tel exige une surface, si tant est que l'objection peut s'élever qu'une pierre
levée, une colonne grecque c'est un signifiant et que ça a un volume, n'en
soyez pas si sûrs, si sûrs de pouvoir introduire la notion de volume avant d'être
bien assurés de la notion de surface. Surtout si, en mettant les choses à l'épreuve,
la notion de volume n'est pas saisissable autrement qu'à partir de celle de
1'enveloppe. Nulle pierre levée ne nous a intéressés par autre chose, je ne
dirai pas que son enveloppe - ce qui serait aller à un sophisme, - mais par ce qu'elle enveloppe.
Avant d'être des volumes,
l'architecture s'est faite à mobiliser, à arranger des surfaces autour d'un
vide. Des pierres levées servent (->p442)
(XX/7) à faire des alignements ou des tables,
à faire quelque chose qui sert par le trou qu'il y a autour.
Car c'est cela le reste à quoi nous
avons à faire. Si, attrapant la nature de la face, je suis parti de la surface
avec bords pour vous faire remarquer que le critère nous défaillait aux
surfaces sans bord, s'il est possible de vous montrer une surface sans bord
fondamentale, où la définition de la face n'est pas forcée, puisque la
surface sans bord n'est pas faite pour faire résoudre le problème de l'intérieur
et de l'extérieur, nous devons tenir compte de la distinction d'une surface
sans
avec une surface avec : elle a le rapport le plus étroit avec ce qui nous intéresse,
à savoir le trou qui est à faire entrer positivement comme tel dans la théorie
des surfaces.
Ce n'est pas un artifice verbal. Dans la
théorie combinatoire de la topologie générale, toute surface triangulable,
c'est-à-dire composable de petits morceaux triangulaires que
vous collez les uns aux autres, tore ou cross-cap, peut se réduire par
le moyen du polygone fondamental à une composition de la sphère à laquelle
seraient adjoints plus ou moins d'éléments toriques, d'éléments de
cross-cap et des éléments purs trous indispensables représentés par ce
vecteur bouclé sur lui-même
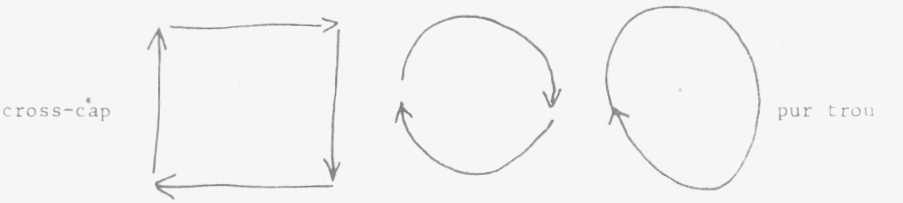
Est-ce
qu'un signifiant, dans son essence la plus radicale, ne peut
Cette
dimension, temporelle du
fonctionnement de la chaîne signifiante que j'ai d'abord articulée comme
succession, a pour suite que la scansion introduit un élément de plus que la
division de l'interruption (->p443) (XX/8) modulatoire : elle introduit la
hâte que
j'ai insérée en tant que hâte en logique. C'est un vieux travail : "le
Temps logique".
Le pas que j'essaie de vous faire
franchir a déjà commencé d'être tracé, c'est celui où se noue la
discontinuité avec ce qui est l'essence du signifiant, à savoir la
différence.
Si ce sur quoi nous avons fait pivoter, nous avons ramené sans cesse cette
fonction du signifiant, c'est à attirer votre attention sue ceci que, même à répéter
le même, le même d'être répété s'inscrit comme distinct. Où est
l'interpolation d'une différence ? Réside-t-elle seulement dans la
coupure -c'est ici que 1'introduction de la dimension topologique
au-delà de la scansion temporelle nous intéresse - ou dans
ce quelque chose d'autre que nous appellerons la simple possibilité d'être
différent, l'existence de la batterie différentielle qui constitue le
signifiant et par laquelle nous ne pouvons pas confondre synchronie avec simultanéité à la racine du phénomène,
synchronie qui fait que réapparaisse
le même ?
C'est comme distinct de ce qu'il répète
que le signifiant
reparaît, et ce qui peut être
considéré
comme distinguable c'est l'interpolation de la différence pour autant que
nous
pouvons poser comme fondamentale de la fonction signifiante l'identité du
"a et a", à savoir que la différence est dans 1a coupure, ou dans
la possibilité synchronique qui constitue la différence signifiante.
En tout cas ce que nous répétons n'est différent
que de pouvoir être inscrit.
Il n'en reste pas moins que la fonction de la coupure nous importe au premier chef dans ce qui peut être écrit. Et c'est ici que la notion de surface topologique doit être introduite dans notre fonctionnement mental parce que c'est là seulement que prend son intérêt la fonction de la coupure.
L'inscription nous ramenant à la mémoire est une objection à réfuter. La mémoire qui nous intéresse, nous analystes, est à distinguer d'une mémoire organique, celle qui a la même succion du réel réponde par la même façon pour l'organisme de s'en défendre que celle que nous tient l'homéostasie, car l'organisme ne reconnaît pas le même qui renouvelle en tant que différent. La mémoire organique mémorise (même-orise) .
(->p444) (XX/9) Notre mémoire est autre chose : elle
intervient en fonction du trait unaire marquant la fois unique et a pour support
l'inscription. Entre le stimulus et la réponse, l'inscription, le printing,
doit être rappelé en termes d'imprimerie gutenbergienne. Le premier jet de la
théorie psychophysique contre lequel nous nous révoltons est toujours
atomistique ; c'est toujours à l'impression dans des schémas de surface que
cette psycho-physique prend sa première base. I1 ne suffit pas de dire
que c'est insuffisant avant qu'on n'ait trouvé autre chose.
Car s'il est d'un grand intérêt de
voir que la première théorie de la vie relationnelle s'inscrit en des termes
intéressants qui traduisent seulement sans le savoir la structure même du
signifiant sous les formes masquées des effets distincts de contiguïté et de
continuité (assocíationnisme), il est bon de montrer que ce qui était reconnu
et méconnu comme dimension signifiante, c'étaient les effets du signifiant
dans la structure du monde idéaliste dont cette psychophysique ne s'est jamais
détachée.
Inversement ce qu'on a introduit par la Gestalt est insuffisant à rendre compte de ce qui se passe au niveau des phénomènes vitaux, en raison d'une ignorance fondamentale qui se traduit par la rapidité avec laquelle on tient pour certaines des coordonnées que tout contredit. La prétendue bonne forme de la circonférence que l'organisme s'obstinerait sur tous les plans - subjectifs ou objectifs - à chercher à reproduire est contraire à toute observation des formes organiques. Je dirai aux Gestaltistes qu'une oreille d'âne ressemble à un cornet, à un arum, à une surface de Moebius. Une surface de Moebius est l'illustration la plus simple du cross-cap : ça se fabrique avec une bande de papier dont on colle les 2 extrémités après l'avoir tordue, de sorte que l'être infiniment plat qui s'y promène peut le suivre sans jamais franchir aucun bord. Ca montre l'ambiguïté de la notion de face. Car il ne suffit pas de dire que c'est une surface unilatère, à une seule face, comme certains mathématiciens le formulent. Autre chose est une définition formelle, il n'en reste pas moins qu'il y a coalescence pour chaque point de 2 faces et c'est ça qui nous intéresse. Pour nous qui ne nous ne contentons pas de la dire unilatère sous prétexte que ces deux faces sont partout présentes, il n'en reste pas moins que nous pouvons manifester en chaque point le scandale pour notre intuition de ce rapport des deux faces.
(->p445) (XX/10)
 |
En effet dans un plan, si nous traçons un cercle dans le sens des aiguilles d'une montre, de 1' autre côté, par transparence, la même flèche tourne dans le sens contraire. L'être infiniment plat, le petit personnage sur la surface de Moebius, s'il véhicule avec lui un cercle tournant autour de lui dans le sens des aiguilles d'une montre, |
ce cercle tournera
tournera toujours dans le même sens, si bien que de l'autre côté de son point de départ ce qui s'inscrira
tournera dans le sens horaire, c'est-à-dire en sens opposé à ce
qui passerait sur une bande normale, sur le plan : ça n'est pas inversé.
C'est pour ça qu'on définit ces
surfaces comme non-orientables et pourtant ça n'en est pas moins orienté. Le désir,
de n'être pas articulable, nous ne pouvons dire pour
autant qu'il ne soit pas articulé.
| Car ces petites oreilles dans la
|
 |
la même forme. Même quand vous retourner l'objet, il y
aura toujours la bosse rentrée sur la gauche, la bosse renflée sur la droite
, une surface non-orientable est donc beaucoup plus orientée qu'une
surface orientable.
Quelque chose vu encore plus loin et
surprend les mathématiciens qui renvoient avec un sourire le lecteur à 1'expérience,
c'est que, si dans cette bande de Moebius à l'aide de ciseaux vous
tracez une coupure à égale distance des points les plus accessibles des bords
(elle n'a qu'un seul bord), si vous faites un cercle, la coupure se ferme, vous
réalisez un cercle, un lacs, une courbe fermée de Jordan. Or cette
coupure, non seulement laisse la surface entière, mais transforme la surface
non-orientable en surface orientable, c'est-à-dire en une bande
dont, si vous colorez l'un des côtés, tout un côté restera blanc, contrairement
à ce qui ce serait passé tout à l'heure sur la surface de Moebius entière : tout aurait été coloré sans que le pinceau change
de face. La simple intervention de la coupure a changé la structure omniprésente
de tous les
Le polygone quadrilatère est originaire
du tore et du bonnet. Si je n'ai jamais introduit la véritable verbalisation de
cette forme &&
, poinçon, désir, unissant le S
au a dans S &
a , ce petit
quadrilatère doit se lire : le sujet en tant que marqué par le signifiant est
propre
La prochaine fois, vous verrez comment
ceci nous donnera un support fonctionnant pour articuler la question ; comment ce
que nous pouvons définir, isoler â partir de la Demande comme champ du désir,
dans son côté insaisissable, peut-il, par quelque torsion, se nouer avec
ce qui, pris d'un autre côté se définit comme le champ de l'objet a, comment
le désir peut-il s'égaler à a. C'est ce que j'ai introduit et qui vous
donnera un modèle utile jusque dans votre pratique.
note: bien que relu, si vous découvrez des erreurs manifestes dans ce séminaire,
ou si vous souhaitez une précision sur le texte, je vous remercie par
avance de m'adresser un émail.
Haut de
Page
commentaire