| |
|
|
Entrelacs, Noeuds, Tresses, Chaines, Echeveau, |
|
|
| |
|
|
|
|
|
| |
|
|
Il n'y a pas de théorie des noeuds à ce jour ! |
|
|
| |
|
|
|
|
|
| |
|
|
Chaine, Chainoeud, Echeveau, Entrelacs,
Noeuds (classique, propre, impropre, mathématique, logique, topologique, ) , Tresse, |
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
Entrelacs |
|
En théorie des nœuds, un entrelacs est un enchevêtrement de plusieurs nœuds. L'étude des entrelacs et des nœuds est liée, plusieurs invariants s'interprétant plus naturellement dans le cadre général des entrelacs, au moyen notamment des relations d'écheveau. |
|
|
| |
|
|
Les entrelacs étudiés sont généralement les entrelacs réguliers, c'est-à-dire tels que chacune de ses composantes est un nœud, mais il existe également une notion d'entrelacs singuliers. On demande en plus que ces nœuds ne soient pas sauvages. Un entrelacs à une seule composante est alors exactement un nœud. |
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
Le théorème d'Alexander stipule que tout entrelacs est représentable par une tresse fermée. |
|
|
| |
|
|
Entrelacs, amp, |
|
|
| |
|
|
|
|
|
| |
Noeud |
|
En mathématiques, et plus particulièrement en géométrie et en topologie algébrique, un nœud est un plongement d'un cercle dans 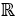 3 3, l' espace euclidien de dimension 3, considéré à des déformations continues près. Une différence essentielle entre les nœuds usuels et les nœuds mathématiques est que ces derniers sont fermés (sans extrémités permettant de les nouer ou de les dénouer) ; les propriétés physiques des nœuds réels, telles que la friction ou l'épaisseur des cordes, sont généralement également négligées. Plus généralement, on parle aussi de nœud pour des plongements de S j dans S n , tout particulièrement dans le cas j = n − 2. L'étude des nœuds mathématiques s'appelle la théorie des nœuds. |
|
|
| |
|
|
|
|
|
| |
& Tresse |
|
le théorème d'Alexander :
Chaque noeud s'obtient de la cloture d'une certaine tresse
. (En fait Alexander a démontré que cette assertion est vraie plus généralement pour les entrelacs, dont les noeuds sont un cas particulier.)
d'après Noeuds, Alexei.SOSSINSKY, Seuil, p42, |
|
|
| |
|
|
|
|
|
| |
Noeud Propre |
|
Fait d'un seul rond. |
|
|
| |
|
|
|
|
|
| |
Noeud Impropre |
|
ou Chaine, Faite de deux ronds ou plus. |
|
|
| |
|
|
|
|
|
| |
|
|
Bien, mais venons-en aux machines. Le Séminaire suivant, le Livre II développe,
me semble-t-il, là cette question des machines que j’ai été très surpris
de rencontrer sous cet aspect dans la mesure ou je les avais étudiées comme
des automates abstraits chez les mathématiciens et puis que j’avais eu l’idée
de ce qu’une machine pouvait être, bien qu’on ne pense pas assez souvent
qu’une poulie ou un dé soit une machine. Et ce vers quoi je voudrais aller,
c’est parler de machines qui sont un petit peu différentes les unes des
autres et parler du nœud et des chaînes comme machines. JMV in LACAN, Séminaire XXVI, TT15051979, |
|
|
|
|
|
|
|
|
| |
Noeud mathématique |
|
Le nœud des mathématiciens est un plongement de cercle, c'est un cercle.
Pour eux, la chaine est un plongement de plusieurs cercles. Certains disent de la chaîne qu'elle est un nœud emboité. C'est dans ce cas une chaîne-nœud. |
|
|
| |
|
|
les mathématiques, c’est pas un métalangage, c’est une système d’écriture qui permet de corriger l’objet, alors où est ce que Lacan nous dit ça ?
Les mathématiques c’est écrit et la théorie des ensembles et l’écriture mathématique permettent de corriger l’objet ! |
|
|
| |
|
|
les nœuds mathématiques ce sont des ronds, ce sont par exemple des déformations topologiques du cercle trigonométrique, le cercle trigonométrique c’est métrique, mais les déformations continues, c’est pas métriques, bien que ce soit passé dans l’histoire de la géométrie, on passe des cercles aux coniques facilement et les ellipses c’est des cercles déformés en continue, voyez les ellipses des planètes et les trajectoires des planètes c’est des ellipses, ce que Kepler va établir, mais on connait les coniques depuis les grecques, comme section du cône par un plan, en faisant bouger le plan, on déforme la section, et les cercles sont des sections perpendiculaires à l’axe du cône, alors que les autres coniques sont obtenues par section du cône si on penche le plan, si on le fait un peu tourner, ça c’est encore métrique, c’est déjà l’idée d’une déformation continue, même en géométrie grecque, |
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
Noeud
classique |
|
Théorie des noeuds classique : c'est la théorie des noeuds physiques, faits avec de la corde, ils peuvent être déformés sans changer leur identité par les composés des trois mouvements de Reidmaster, T1, B2, T3. |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
les nœuds logiques |
|
ils sont plus proches de l’écriture, c’est un chemin propédeutique pour étudier les nœuds topologiques, qui eux sont plus proches de la parole,
-Un noeud logique est un plongement du noeud trivial (un cercle- voir ci-dessous) de la logique classique, dans la logique modifiée en topologie du sujet. Ce noeud reste dominé par la Loi de la Parole, l'impératif du dire .... |
|
|
| |
|
|
|
|
|
| |
|
|
Un nœud logique c’est un plongement de la logique classique, V01-32.23 ; que j’écris comme ça, c’est le nœud le plus simple que j’écris (0,1), on va appeler ça le nœud trivial, mais avec toute l’algèbre linéaire qui est booléenne, et qui se développe à partir de ce 0 et ce 1.Mais les deux termes, les deux constantes c’est 0 et 1. Donc c’est l’algèbre de Z2;, Z c’est les deux classes d’équivalences, des nombres pairs et des nombres impairs, Z2, c’est modulo 2, c’est Z2, qui est égal à l’ensemble (0.1), muni d’une addition et d’une multiplication, et ça c’est une algèbre de Boole et c’est même un corps de Boole, c’est le seul corps de Boole, les corps ensuite si on prend les puissance de Z2, on va avoir les algèbres de Boole et pas des corps, et René Guitart a montré quand faisant ces extensions du corps de Boole, on obtenait des corps de Galois, qui sont liés aux algèbres de Boole, ce qui fait un très beau résultat, il fait un lien entre Boole et Galois, on ne va pas parler de ça, mais c’est quand même assez élégant à notre époque de voir que les deux grands algébristes de XIX siècles se trouvent comme ça en correspondance, c’est assez satisfaisant, pour le lecteur de découvrir qu’il y a un lien entre la logique , l’algèbre de la logique, l’algèbre de Boole et les corps de Galois de caractéristique 2, 35.19, ce qui fait que ça va pouvoir s’étendre dans ce qu’on va appeler les nœuds logiques non triviaux, V01-34.17 ;
Si je prends maintenant deux valeurs dans l’algèbre de Boole qui n’est pas triviale, 35.32, alors ici je prends, je vais avoir un nœud logique, ça ( S1) c’est le rond de ficelle, pour que vous arriviez à suivre le raisonnement, dans les nœuds topologiques, ici, vous avez le nœud trivial, c’est un rond déformable, ça c’est trivial, V01-34.51 ; le nœud trivial, là aussi c’est au pluriel, il y a des nœuds topologiques, le nœud trivial, et vous pouvez avoir un nœud comme ça, déformés, je choisis celui là, je choisis le nœud de Trèfle, ça commence avec le nœud de trèfle, celui là à 6 croisements, ça commence avec celui là, (le trèfle) ceux là ce sont des nœuds non triviaux, des nœuds propres, faits d’un seul fil, à gauche c’est le nœud trivial, c’est le nœud zéro, 0, alors ici vous avez (u, V) pour les nœuds logiques, vous avez des nœuds logiques, pour n’importe quel (u, V), il faut se placer dans une algèbre de Boole qui est plus grande, qui s’appelle Z2n; = [(0,1)n; , +uV, xuV] comment créer ce plongement que j’appelle psy, Y u,V, comment balancer la logique classique avec tout ce qui suit, et qu’on va regarder, en particulier avec le fait qu’on y trouve l’aliénation, comme étant une condition nécessaire de la logique classique, l’aliénation au sens ou Lacan la définit, et tout ce qui est ici (à gauche) doit se trouver développé là, (à droite) , mais comment on passe de l’un à l’autre par une fonction que j’appelle (psy) Ψ.; ΨuV ; V01-37.03 ... JMV20150602 |
|
|
| |
|
|
|
|
|
| |
|
|
il est un plongement de la logique classique dans une logique plus grande, dans une Algèbre de Boole plus grande, au lieu d’être uniquement dans Z2, comme ça, Z2 c’est 0,1, avec l’addition et la multiplication, +, x, c’est un anneau de Boole, et celui là c’est le plus petit, c’est un corps de Boole, et si on plonge cette logique classique, tout ce qu’on fait avec ce 0 et ce 1 ; dans Z2 puissance n, Z2n, donc vous avez 0, 1, à la puissance n, et vous avez + et x, là c’est plus un corps ce sont des anneaux de Boole, mais Guitart a montré qu’à partir de là, on pouvait aussi faire des extensions de corps, donc à partir de Z2, le plus petit, et qu’on obtenait des corps de Galois, ça s’appelle GaloisField en anglais, 59.37, 2 puissance n, 2n, de caractéristique 2, vous voyez que le 2 joue un rôle, mais ne confondez pas ce 2 qui ici, est un élément qui est dit caractéristique, la caractéristique c’est le nombre qui multiplie n’importe quel élément pour donner zéro, donc l’algèbre de Boole, que ce soit la plus petite qui est un corps, ou les anneaux de Boole et les Algèbres de Boole la structure linéaire, ça c’est de caractéristique 2, et les corps de Galois de caractéristique 2 correspondent à des Algèbres de Boole, ça on peut appeler ça Algèbre de Boole, AB (2n), des algèbres de Boole de plus grand cardinal que simplement 2, ici, vous avez une toute petite algèbre avec 0,1, (nœud logique), seulement, 1.00.29, je vous ai écrit au tableau les deux formules du plus et du multiplier, le plus c’est o, 1 qui va nous donner 0, 1 et ici du 0, je répète que je vous ai donné un moyen de rendre ça plausible, pour votre pratique, pour que vous ayez les coudées franches pour pourvoir apprendre à compter, à faire de l’algèbre de Boole sans être un ordinateur, sans être obligé de vous transformer en automate,.. .JMV23062015, L475; |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
Noeud topologique |
|
les nœuds topologiques, qui eux sont plus proches de la parole, pourquoi ? parce que dans les nœuds topologiques ça ressemble à une écriture et on se goure tout le temps, ça c’est une hypothèse que je fais, Lacan a cherché un endroit, il doit bien y avoir un lieu, où parole et écriture se rencontrent puisque ce sont deux inerties différentes, l’inertie de l’écriture ça se corrige, l’inertie de la parole c’est incorrigible, et de fait une fois qu’on a dit quelque chose on ne peut pas le corriger, on peut omettre une objection, mais ce qui a été dit est dit, le problème c’est la fonction de l’énonciation, |
|
|
| |
|
|
|
|
|
| |
|
|
Le noeud est un accomplissement de coupure. Noeud, p161, J-M.VAPPEREAU,
- Les noeuds (ou chaines) ne sont perceptibles que d'une position extrinsèque, et relève de ce narcissisme "externe" : je vois mon image dans le miroir, et tout à a fois je suis dans la réalité du territoire.
|
|
|
| |
|
|
|
|
|
| |
|
|
Le nœud représente ce qui fait tenir le nœud dans la chaîne.
- le nœud topologique il va être fait avec une courbe qui se déforme plus que le cercle et l’ellipse, mais qui est un cercle déformé qui n’est pas rigide, |
|
|
| |
|
|
|
|
|
| |
|
|
Un noeud topologique est un plongement du noeud trivial. Le noeud trivial c'est le cercle trigonométrique défini de manière analytique sur le plan par l'équation à deux variables celui du " pont aux ânes" classique (x2 + y2 = 1), mais en abandonnant l'invariant euclidien de la mesure pour priviliégier la différence de la topologie définie par le couple : continu ou discret : connexe ou non connexe (coupé). |
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
Tresse |
|
En mathématiques, et plus précisément en topologie et théorie des groupes, une tresse est un objet mathématique formalisant ce qu'on appelle tresse (ou natte) dans la vie courante. Les tresses ont une structure de groupe naturelle, et possèdent des liens profonds avec des domaines divers des mathématiques notamment en topologie, théorie des nœuds et combinatoire algébrique. Cette théorie trouve des applications en physique statistique, en mécanique quantique ainsi qu'en informatique théorique, par exemple en cryptographie. |
|
|
| |
|
|
|
|
|
| |
|
|
le théorème d'Alexander :
Chaque noeud s'obtient de la cloture d'une certaine tresse
. (En fait Alexander a démontré que cette assertion est vraie plus généralement pour les entrelacs, dont les noeuds sont un cas particulier.)
d'après Noeuds, Alexei.SOSSINSKY, Seuil, p42,
|
|
|
| |
|
|
|
|
|
| |
|
|
Tresses, matematita.science, & lire : Tresses en mouvements, images.math.cnrs,
1 : le premiere chapitre on formalise les tresses comme objets topologiques et algébriques.
2 : le seconde chapitre on considére le problème si deux tresses sont equivalentes, c’est-à-dire si on peut passer de l’une à l’autre par une déformation sans qu’un brin ne passe à travers l’autre.
3 : le troisième chapitre on considére des relations entre les nœuds et les tresses.
4 : le quatrième chapitre on considére des danses et on le relie aux tresses. |
|
|
| |
|
|
|
|
|
| |
Chaine |
|
Pour eux, (les mathématiciens) la chaine est un plongement de plusieurs cercles. Certains disent de la chaîne qu'elle est un nœud emboité. C'est dans ce cas une chaîne-nœud. |
|
W, |
| |
|
|
Faite de deux ronds ou plus, |
|
|
| |
Chainoeud |
|
- linknots, ou Noeud impropre, pour les chaines à coupure constantes, exemple du Noeud borroméen avec ses quatre coupures. Ces chainoeuds ne contiennent aucun enlacement. Noeud p109 |
|
|
| |
|
|
|
|
|
| |
|
|
Or je dis qu’après dans ce séminaire XX, après avoir articulé
précisément à propos du mathème la
borne par-dessus laquelle le mathématicien qui fait le calcul des prédicats
n’est pas obligé de sauter, eh bien, on rencontre les chaînes, c’est-à-dire
on revient aux machines, on quitte ces modèles et la théorie des ensembles même
plus mécanisée et on revient à des machines beaucoup plus simples. Et c’est
des machines beaucoup plus simples qui me semblent avoir un intérêt à être
pratiquées,
JMV in LACAN, Séminaire XXVI, TT15051979 |
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
Echeveau |
|
Relation d'écheveau, skein relation, |
|
|
| |
|
|
Les relations d'écheveau sont un outil mathématique utilisé pour étudier les nœuds. Une question centrale dans la théorie mathématique des nœuds est de savoir si deux diagrammes de nœuds représentent le même nœud. Une façon de répondre à la question consiste à utiliser des polynômes de nœuds, qui sont des invariants du nœud. Si deux diagrammes ont des polynômes différents, ils représentent des nœuds différents. En général, l'inverse ne tient pas.
Les relations en écheveau sont souvent utilisées pour donner une définition simple des polynômes de nœuds. Une relation d'écheveau donne une relation linéaire entre les valeurs d'un polynôme de nœud sur une collection de trois liens qui ne diffèrent les uns des autres que dans une petite région. Pour certains polynômes de nœuds, tels que les polynômes de Conway, d'Alexander et de Jones, les relations d'écheveau pertinentes sont suffisantes pour calculer le polynôme de manière récursive. |
|
Traduction google, |
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|