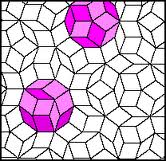
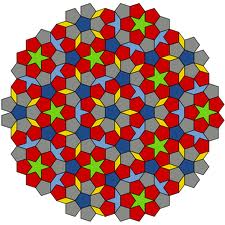
Les idées de symétrie et de régularité précèdent la notion de groupe dans la civilisation
(ex : - il y a 17 types, non isomorphes, sous-jacents aux multiples ornements géométriques imaginés par les artistes arabes. – Chez les grecs les propriétés de régularité trouvent un aboutissement dans les Eléments d'Euclide par la constitution des 5 polyèdres réguliers, soit la détermination des groupes finis de rotations dans l'espace à 3 dimensions).
La notion de groupe n'apparaît qu'au cours de travaux sur la résolution d'équations algébriques « par radicaux », au début du XIXe siècle, où les groupes de permutations des racines d'une équation algébrique laissent invariantes certaines fonctions de ces racines.
Les premiers groupes sont des groupes finis, et c'est sous la forme de la théorie des groupes de permutations que la théorie générale des groupes finis commencera à se développer, jusqu'en 1870.
La cristallographie mathématique vers 1830 font apparaître d'autres groupes finis formés de rotations et de symétries laissant un point fixe et JORDAN en 1868 aborde l'étude des groupes de déplacement ( finis ou non) dans l'espace euclidien à trois dimensions.
Puis KLEIN et POINCARRE feront des groupes de déplacements non euclidiens le fondement de leur théorie des fonctions automorphes, et LIE, cherchant à réaliser pour les équations différentielles ce que GALOIS avait fait pour les équations algébriques, crée la théorie générale des groupes continus de transformations (appelés groupe de LIE ).

KLEIN au sujet des fondements de la Géométrie élémentaire met la notion de groupe de transformations à la base même de cette branche des mathématiques, qui devient un simple chapitre de la théorie des groupes classiques développés par JORDAN à la fin du XIXe siècle.
Alors la structure de groupe comme nous la concevons aujourd'hui est définie de façon intrinsèque ( et non plus dans le seul cas ou les éléments du groupe sont des transformations).
Depuis la notion de groupe a envahi toutes les mathématiques contemporaines.

Débordant le concept initial de groupe «  ensembliste » ( groupe topologiques , groupe algébriques , schémas en groupes, « objets » en groupe d'une catégorie représentant un foncteur représentable de cette catégorie dans la catégorie des groupes), on découvre alors des relation imprévues entre les groupes de Lie, les groupes algébriques, les groupes arithmétiques, et les groupes finis).
La notion de groupe est très efficace dans toutes les parties des mathématiques une fois qu'on parvient à l'y introduire : groupe d'homologie et d'homotopie en topologie algébrique, espaces fibrés principaux en géométrie e topologie différentielle. Ou la possibilité de définir une structure de groupe sur l'ensemble des classes de structures différentielles compatibles avec une variété (topologique) donnée.

Cette tendance a gagné la physique en cherchant à expliquer les symétries expérimentales des phénomènes atomiques, ce avec un succès remarquable et fort mystérieux !!

( d'après)
Jean DIEUDONNE, p516, Encyclopaedia Universalis, Dictionnaire des Mathématiques