13
Solides de



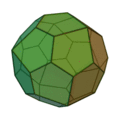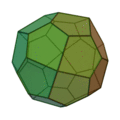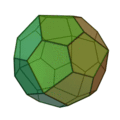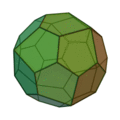
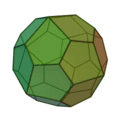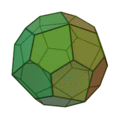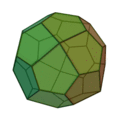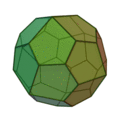
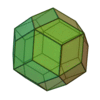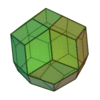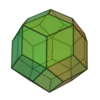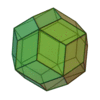
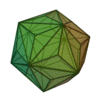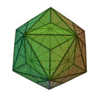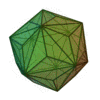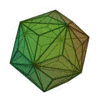





(deux formes chirales)
pentagonal (deux formes chirales)
| Ouverture Polygones Polyèdres Platon Kepler-Poinsot Archimède Catalan Johnson Trapèzes Pyramides Diamants Polychores Schafly Polytopes Révolution | |||||||||||||||
| vers D3 | 13 |
Solides de |
CATALAN | D3 | |||||||||||
| D3 |  |
 |
 |
 |
 |
 |
  |
 |
 |
 |
 |
 |
  |
||
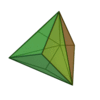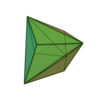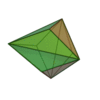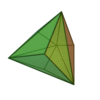
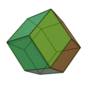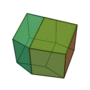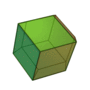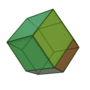
| Invariants | Triakitétraèdre | Dodécaèdre rhombique | Triakiotaèdre | Tétrakihexaèdre | Icositétraèdre trapézoïdal | Hexakioctaèdre | Icositétraèdre pentagonal (deux formes chirales) |
Triacontrèdre rhombique | Triaki-icosaèdre | Pentakidodécaèdre | Hexaontrèdre trapézoïdal | Hexaki icosaèdre | Hexacontaèdre pentagonal (deux formes chirales) |
||
| Type | Solides de Catalan | ||||||||||||||
| Type de face | triangle isocèle | losange | triangle isocèle | triangle isocèle | Trapèze | Triangle scalène | pentagones irrrégulier | Losange | Triangle isocèle | triangle isocèle | Trapèze | Triangle scalène | Triangle irrégulier | ||
| Configuration de sommets | V3,6,6 | V3,4,3,4 | V3,8,8 | V4,6,6 | V3,4,4,4 | V4,6,8 | V3,3,3,4 | V3,5,3,5 | V3,10,10 | V5,6,6 | V3,4,5,4 | V4,6,10 | V3,3,3,5 | ||
| faces | 12 | 12 | 24 | 24 | 24 | 48 | 24 | 30 | 60 | 60 | 60 | 120 | 60 | ||
| arêtes | 18 | 24 | 36 | 36 | 48 | 72 | 60 | 60 | 90 | 90 | 120 | 180 | 150 | ||
| sommets | 8 | 14 | 14 | 14 | 26 | 26 | 38 | 32 | 32 | 32 | 62 | 62 | 92 | ||
| caractéritique E-P : χ =S-A+F (khi) | |||||||||||||||
| Symbole de Schläfli | |||||||||||||||
| Symbole de Wythoff | |||||||||||||||
| Diagramme de Coxeter-Dynkin | |||||||||||||||
| Références d'indexation (à indicier) | |||||||||||||||
| Dual (solides d'Archimède) | Tétrèadre tronqué | Cuboctaèdre | Cube tronqué | Octaèdre tronqué | Petit rhombicuboctaèdre | Grand rhombicuboctaèdre | Cube adouci | Icosidodécaèdre | Dodécaèdre tronqué | Icosaèdre tronqué | Petit rhombicosaèdre | Grand rhombicododécaèdre | Dodécaèdre adouci | ||
| Groupe de Symétrie | Td | Oh | Oh | Oh | Oh | Oh | O | Ih | Ih | Ih | Ih | Ih | I | ||
| Propriétés | |||||||||||||||
| graphe | |||||||||||||||