
Version
rue CB
note
21
Novembre 1978
(p1->)Il
y a une correspondance entre la
topologie et la pratique. Cette correspondance consiste en les temps. La
topologie résiste, c’est en cela que la correspondance existe.
Il y a
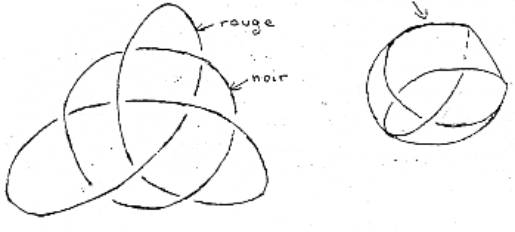
une bande de Moebius que nous avons tracée (1). C’est ce qu’on appelle une
bande triple. On peut remarquer que cette bande triple, ce qui la caractérise,
c’est qu’elle a des bords
et que ses bords sont à peu près comme ceci (2) :

(1)
(2)
(p2->)
Si vous rabattez ces bords, vous obtenez quelque chose qui se présente comme ça :
 Et
le cercle noir prend alors cet aspect là.
Et
le cercle noir prend alors cet aspect là.
Voilà
à peu près ce que ça donne.
Ici
le cercle noir est blanc. (Il montre un montage fait d’un anneau de cordelette
blanche passant à l’intérieur d’un enroulage de cordelette jaune). Voilà,
je vous le passe.
Il
y a une façon, de cette bande, de la couvrir. Après ça, ça passe derrière
la bande suivante.
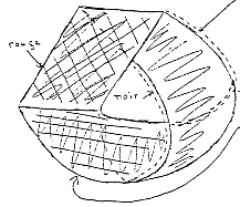 dire
derrière la bande de Moebius triple.
dire
derrière la bande de Moebius triple.
C’est
pourquoi ça revient en avant. De sorte que ce qu’on a, c’est :
(1
2)
En
avant
(3
4) derrière 6
(5
6)
qui
rejoint le 1.
C’est
bien ce que j’ai, de la bande enveloppante, marqué- vous pouvez la manipuler
et même en recouvrir la bande triple. Vous avez ici un autre exemplaire de ce
que j’ai appelé pour l’instant la bande enveloppante. Vous pouvez en
constater l’identité avec…
Ce
qu’il y a de frappant, c’est que la bande de Moebius normale – voilà un
exemple :
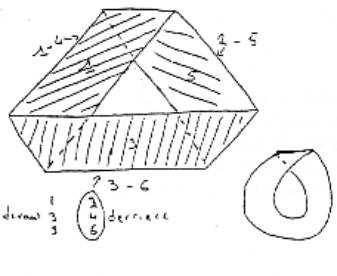 -une
bande de Moebius normale, c’est à dire une bande de Moebius comme ça, a également
le 1 et le 2 et le 3 et le 4 à la même place. Tous ceux-là derrière et ceux-là sont devant. Voilà le 1, il passe
derrière ici au 2 et il passe devant le 3. Au 4, il passe derrière, ce qui lui
permet de revenir devant le 5 et de passer par derrière pour rejoindre le 1 par
ce qu’on appelle le 6.
-une
bande de Moebius normale, c’est à dire une bande de Moebius comme ça, a également
le 1 et le 2 et le 3 et le 4 à la même place. Tous ceux-là derrière et ceux-là sont devant. Voilà le 1, il passe
derrière ici au 2 et il passe devant le 3. Au 4, il passe derrière, ce qui lui
permet de revenir devant le 5 et de passer par derrière pour rejoindre le 1 par
ce qu’on appelle le 6.
C’est
un point important, vous pourrez le contrôler sur ce que je vous ai fait
circuler à l’instant.
Il
y a quelque chose de commun entre toutes les bandes de Moebius, ne serait-ce que
cette alternance. Est-ce qu’il est possible- c’est certain- de couper les
bandes de Moebius ? Non seulement on peut couper chacune, mais on peut
couper aussi ce que j’appelle la doublure.
Qu’est
ce que la doublure ? Il peut y avoir une doublure toute seule. Mais dans ce
cas, il faut couper la bande de Moebius, la bande de Moebius qui est en somme
l’âme de l’affaire.
Il
y a un moyen de tracer sur un tore une bande de Moebius. Voilà comment on le
trace si il s’agit de la bande à trois.
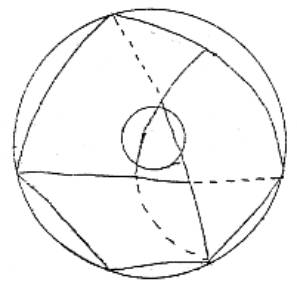 Il
faut pour cela pincer le tore et accoler les deux surfaces qui sont celles du
tore. La face intérieure disparaît, elle est tamponnée, écrasée. Il est
aussi facile de faire avec le tore une bande à trois, ce que je voulais dire,
c’était qu’il était aussi facile de faire une bande à un.
Il
faut pour cela pincer le tore et accoler les deux surfaces qui sont celles du
tore. La face intérieure disparaît, elle est tamponnée, écrasée. Il est
aussi facile de faire avec le tore une bande à trois, ce que je voulais dire,
c’était qu’il était aussi facile de faire une bande à un.

Il
y a quand même une béance entre la psychanalyse et la topologie. Ce dont je
m’efforce, c’est cette béance, de la combler. La topologie est exemplaire,
elle permet dans la pratique de faire un certain nombre de métaphores. Il y a
une équivalence entre la structure et la topologie. C’est ça, le Ca dont il
s’agit dans Groddeck, c’est ça qui est Ca.
(p4->)
Il faut s’orienter dans la structure. Il n’y a pas que les nœuds borroméens.
Pour généraliser ce qu’on appelle les nœuds borroméens, il peut y avoir
une façon de faire qui ne fait pas qu’un nœud soit, en en coupant un, libéré
de tous les autres. Il y a une certaine façon de préciser que, en en coupant
deux sur cinq, c’est très précisément ce qui nécessite que les trois qui
restent soient libres. C’est ce qu’on appelle la généralisation des nœuds
borroméens. En en coupant deux sur cinq, les trois autres sont libres.
J’essaierai de vous en donner un exemple d’ici la fin de l’année.
Voilà,
j’ai parlé une heure. Je vous remercie de votre attention.

note:
bien que relu, si vous découvrez des erreurs manifestes dans ce séminaire, ou
si vous souhaitez une précision sur le texte, je vous remercie par avance
de m'adresser un email. Haut
de Page