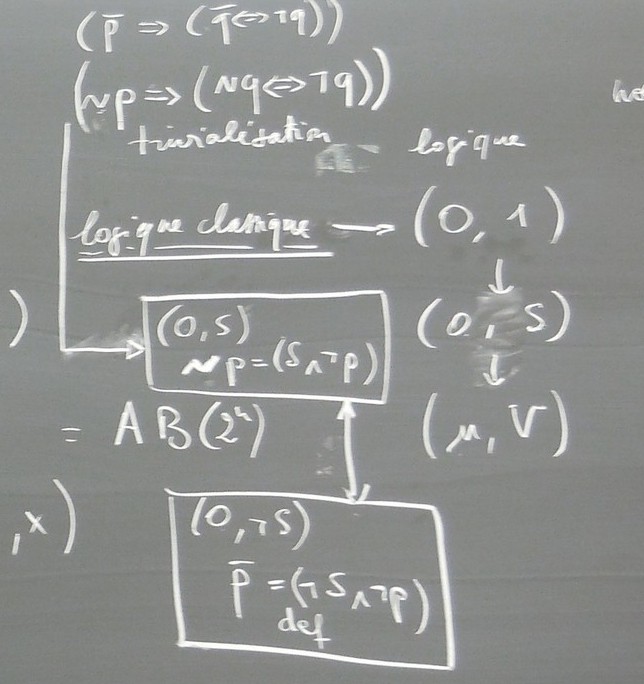08-09-2009
02-06-2015
16-06-2015
voir 1- 2 - 3
Logique de Boole
& voir 1, 2, 3,
& Les noeuds logiques de manières intrinsèque, la logique classique et la logique modifié sont des algèbres de Boole, .pdf, JMV2015, .pdf,
Boole a écrit son calcul pour écrire ce composant là ( les concepts), une partie de ce composant, et en fin de compte tout le monde le retient pour écrire ce composant là ( la calcul de la coordination) actuellement, donc ça crée une grande confusion dont Quine parle très bien, il a consacré dans ses quatre chapitres de Méthode de Logique, le premier chapitre, c’est le calcul de la coordination, le deuxième chapitre c’est le calcul des prédicats monadique et la troisième partie, c’est le calcul des prédicats, et ça va aller vers la théorie des ensembles, quatrième partie, Quine le troisième système qu’il va introduire, c’est la théorie des ensembles, S0T0.
Algèbre de Boole et Théorie de la coordination et Théorie des ensembles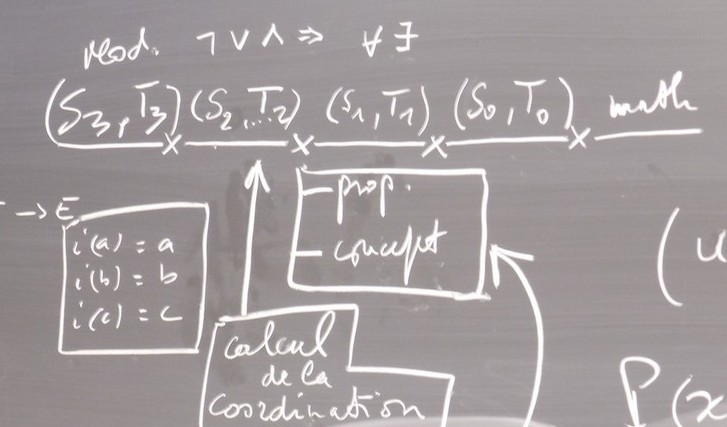
JMV16062015
qu’est que c’est qu’un diagramme d’Euler-Venn, c’est quelque chose qui correspond aux Tables de Vérité,
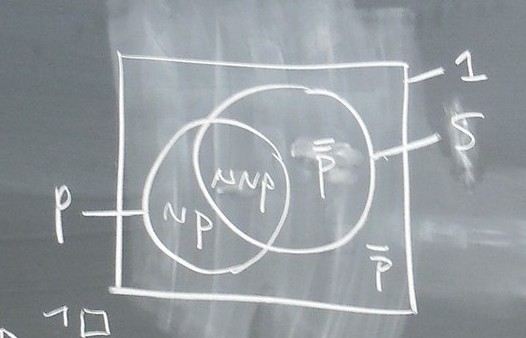
c’est pas un graphisme ensembliste, ça ressemble aux concepts et ça identifie les propositions et les concepts à cause de la coordination qui coordonne aussi bien les propositions que les concepts, et c’est des lectures différentes déjà, si vous lisez les propositions ou si vous lisez les concepts, quand vous avez un cercle, si c’est un concept P (x), c’est-à-dire que vous avez plein d’éléments ici qui sont dans l’extension du concept, qu’on appelle une classe, le concept, dans la théorie des ensembles chez Krivine on appelle ça aussi un collection, c’est la fonction propositionnelle de Frege, ça correspond à plein d’éléments qui sont entourés par le cercle p, qui n’est pas un ensemble, dans la théorie des ensembles ça va être une spécification ça, 1.12.45, ça va être plus compliqué, là vous avez la coordination des concepts si vous faites jouer ce rôle au cercle, mais si au contraire, c’est dedans ici, et dehors, ici il y a bien sûr un dehors, il y a des éléments qui ne sont pas, qui ne tombent pas sous le concept, si vous avez un dedans et un dehors vous avez ici, une proposition p, et dans le dedans c’est p, et dans le dehors c’est non p, ce qui se traduit dans les diagrammes d’Euler-Venn par des hachures et là vous allez voir apparaître les difficultés de la logique, de toute cette logique qui est formidable, qui est très instructive pour ce qui est du sujet que nous étudions, dans notre propre cas, lorsqu’on fait sa psychanalyse, c’est-à-dire qu’il ne s’agit pas d’étudier ça chez les autres, c’est pas de la psychologie, c’est de voir quelles sont les difficultés que nous avons avec ça, comme on va dessiner le diagramme de p, je vous l’ai déjà montré, on va hachurer ce qui est non p,
Et je vous dis que l’affirmation et la négation, ne croyez pas qu’il s’agit que d’une simple complémentarité ensembliste, c’est que la complémentarité ensembliste qui apparaît là, (en bas de l’image vers la droite) par exemple ici, pour non p, (¬p), voyez ici vous avez p, ici vous avez 1, et ici vous avez le diagramme de (non p), ¬p, ça c’est non p, pourquoi et bien parce que la table de vérité de p, vous avez 0 et 1 ici, (à gauche du diagrammes), ça veut dire que ici vous avez 0 c’est dehors, et 1 c’est dedans, et ici vous avez p, sa table de vérité pour p faux c’est faux et quand p est vrai c’est vrai, vous avez ici les hachures c’est 0, et ce qui reste blanc c’est 1, donc qu’est ce que vous constatez et là, ça va êtres le même truc ici, donc vous voyez déjà que ce n’est pas un code, pourquoi c’est pas un code, voyez pourquoi c’est con de confondre ça avec, l’algèbre de Boole a un modèle électrique, ok, et on l’utilise dans les ordinateurs mais c’est complètement con de croire qu’il s’agit d’un jeu d’écriture automatique, parce que si ici, vous avez 0 et là 1, bon 0 c’est les hachures, p c’est le cercle et qui indique qu’il y a quelque chose qui est dedans, et dehors, donc déjà, 1.15.27,
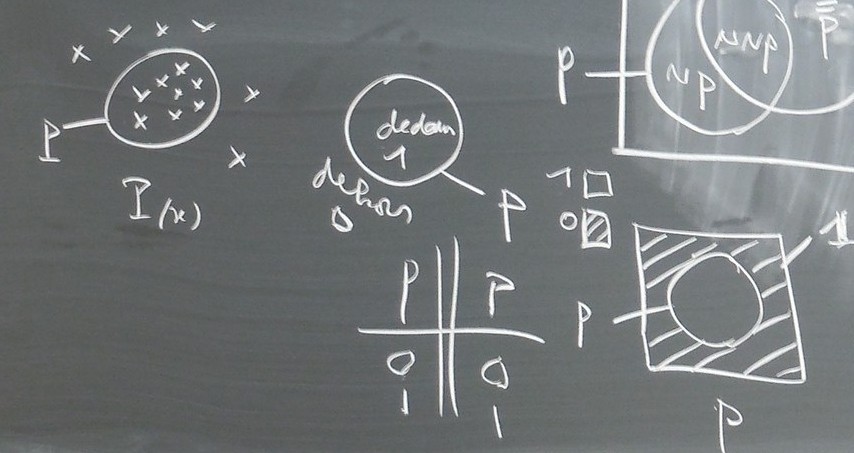
donc déjà vous avez deux usages du 0 et du 1 entre l’indication des zones ( à gauche dans la table de vérité) et l’indication des valeurs, ( à droite dans la table de vérité) ( avec une double barre pour séparation) et quoi d’autre en plus, si vous dites que le blanc n’est pas hachuré, le contraire de la hachure, c’est 1, vous avez deux 1, parce que vous avez le référent qui est 1, ( le 1 du carré complet) alors bien sûr qu’on peut le distinguer, ça va être même toute la question de l’énonciation, ce qui est tautologique, ce qui ne peut se dire, ce qui est correcte, c’est de parler, c’est de n’énoncer que des énoncés vrais, c’est d’ailleurs parce que moi je suis un mauvais élève, les profs de math que nous avons eus, sont incapables d’écrire au tableau des choses fausses, puisqu’ils n’écrivent dans leurs cours que des choses qui sont éprouvées, mais il est un fait que ce sont deux exercices différents de lecture, que de considérer que le 1 c’est le référent, c’est-à-dire que si vous faites l’union de p et de ¬ p, vous allez bien avoir ça, 1.16.45, le diagramme de p∨¬ p ça va vous donner ça, et
là il n’y pas de hachures,  , l’union de ça :
, l’union de ça : 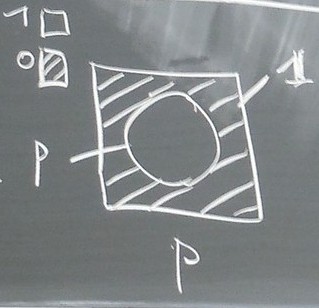 et l’union de ça :
et l’union de ça : 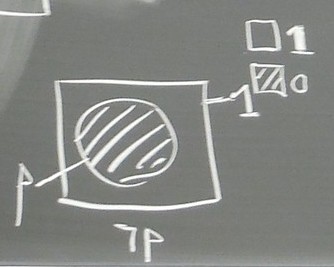 ,
,
V02 16.19, mais voyez ça prête déjà à une erreur qui va faire croire que toute cette logique de la coordination c’est de la théorie des ensembles, c’est-à-dire que c’est la coordination des sous-ensembles d’un ensemble avec la complémentarité, avec l’union, avec l’intersection, mais je vous signale je vous ai dit ça plusieurs fois, que c’est plutôt la théorie des ensembles qui utilise les connecteurs, mais les connecteurs, et surtout si vous voulez analyser sérieusement la négation, vous verrez que c’est quelle que chose qui est différent, qui est beaucoup plus riche que simplement la complémentarité, ou l’algèbre à l’intérieur du treillis des parties des sous ensembles d’un ensemble, des parties d’un ensemble, bien sûr que la théorie de la coordination joue dans mais on ne peut pas réduire cette logique de la coordination dans la langue à la théorie de ensembles, mais ça c’est une erreur qu’on commet beaucoup, alors qu’est ce que je suis en train de vous dire, je suis en train de vous dire qu’il y a toute une zone de développement qui va nous conduire à la logique modifiée, ( grand geste de la zone gauche du tableau jusque vers la zone droite, des deux rectangles) mais que la logique modifiée finalement elle est pleine de pièges, le premier piège c’est l’axiome de A.van Bellinghen, par exemple pour introduire ce caractère supplémentaire, ~, dans la logique modifiée,
( dans le premier rectangle blanc, puis écriture au dessus,)